在第一部分中未應(yīng)用錐削，且從圖中可以看出第一旁瓣為–13 dBc。錐削提供了一種減少天線旁瓣的方法，但會(huì)降低天線增益和主瓣波束寬度。在簡(jiǎn)要介紹錐削之后，我們會(huì)詳細(xì)說(shuō)明與天線增益相關(guān)的幾個(gè)要點(diǎn)。

 

傅里葉變換：矩形函數(shù) ↔ sinc函數(shù)

 

在電氣工程中，有各種不同的方法可以將一個(gè)域中的矩形函數(shù)轉(zhuǎn)變?yōu)榱硪粋€(gè)域中的sinc函數(shù)。最常見(jiàn)的形式是時(shí)域中的矩形脈沖轉(zhuǎn)換成sinc函數(shù)的頻譜分量。這個(gè)轉(zhuǎn)換過(guò)程是可逆的，在寬帶應(yīng)用中，寬帶波形也可以轉(zhuǎn)換為時(shí)域中的窄脈沖。相控陣天線也具有類似的特性：沿陣列平面軸的矩形加權(quán)按照正弦函數(shù)輻射方向圖。

 

應(yīng)用到此特性，以sinc函數(shù)表示的第一旁瓣只有-13dBc是有問(wèn)題的。圖1顯示了這個(gè)原理。

 

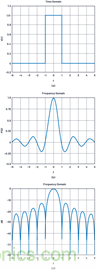
圖1.時(shí)域中的矩形脈沖在頻域中產(chǎn)生正弦函數(shù)，第一旁瓣僅為–13 dBc。

 

錐削（或加權(quán)）

 

要解決旁瓣問(wèn)題，可以在整個(gè)矩形脈沖內(nèi)使用加權(quán)處理。這在FFT中很常見(jiàn)，相控陣中的錐削選項(xiàng)則是直接模擬了FFT中加權(quán)。遺憾的是，加權(quán)也是存在缺點(diǎn)的，它雖然實(shí)現(xiàn)了減少旁瓣但需要以加寬主瓣為代價(jià)。圖2顯示了一些加權(quán)函數(shù)示例。

 

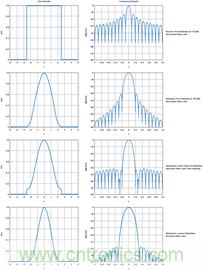
圖2.加權(quán)函數(shù)示例。

 

波形與天線類比

 

從時(shí)間到頻率的轉(zhuǎn)換是很平常的，大多數(shù)電氣工程師自然會(huì)明白。但是，對(duì)于剛接觸相控陣的工程師來(lái)說(shuō)，如何使用天線方向圖類比在一開(kāi)始并不明確。為此，我們用場(chǎng)域激勵(lì)代替時(shí)域信號(hào)，并用空間域代替頻域輸出。

 

時(shí)域 → 場(chǎng)域

 

●   v(t)—電壓是時(shí)間的函數(shù)

●   E(x)—場(chǎng)強(qiáng)與孔徑中的位置呈函數(shù)關(guān)系

 

頻域 → 空間域

 

●   Y(f)—功率譜密度是頻率的函數(shù)

●   G(q)—天線增益是角度的函數(shù)

 

圖3顯示了這些原理。在這里，我們比較了陣列中應(yīng)用兩種不同加權(quán)的輻射能量。圖3a和圖3c顯示場(chǎng)域。每個(gè)點(diǎn)表示這個(gè)N = 16陣列中一個(gè)元件的振幅。在天線之外，沒(méi)有輻射能量，輻射從天線邊緣開(kāi)始。在圖3a中，場(chǎng)強(qiáng)出現(xiàn)突變，而在圖3c中，場(chǎng)強(qiáng)隨著距離天線邊緣的距離增大而逐漸增大。對(duì)輻射能量造成的影響分別如圖3b和圖3d所示。

 

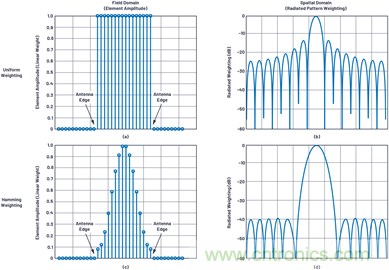
圖3.顯示變窄元件轉(zhuǎn)化為輻射能量加權(quán)的圖表；(A)對(duì)所有元件使用統(tǒng)一加權(quán)；(b)正弦函數(shù)在空間內(nèi)輻射；(c)對(duì)所有元件使用海明窗加權(quán)處理；以及(d)以加寬主波束為代價(jià)，將輻射旁瓣降低到40 dBc。

 

在下一節(jié)中，我們將介紹影響天線方向圖性能的兩種附加誤差項(xiàng)。第一種是互耦。在本文中，我們只是提出存在此問(wèn)題，并且給出用于量化此影響的EM模型的數(shù)量。第二種是由于在相移控制中精度有限而產(chǎn)生的量化旁瓣。我們對(duì)量化誤差進(jìn)行了更深入地處理，并對(duì)量化旁瓣進(jìn)行了量化。

 

互耦誤差

 

這里討論的所有方程和陣列因子圖都假設(shè)元件是相同的，并且每個(gè)元件都具有相同的輻射方向圖。但事實(shí)并非如此。其中一個(gè)原因是互耦，即相鄰元件之間耦合。元件分散在陣列中與元件彼此緊密排列相比，其輻射性能會(huì)發(fā)生很大變化。位于陣列邊緣的元件和位于陣列中心的元件所處的環(huán)境不同。此外，當(dāng)波束轉(zhuǎn)向時(shí)，元件之間的互耦也會(huì)改變。所有這些影響會(huì)產(chǎn)生一個(gè)附加的誤差項(xiàng)，需要天線設(shè)計(jì)人員加以考慮，在實(shí)際設(shè)計(jì)中，需要花大量精力使用電磁仿真器來(lái)表征這些條件下的輻射影響。

 

波束角度分辨率和量化旁瓣

 

相控陣天線還有另一個(gè)缺陷，用于波束轉(zhuǎn)向的時(shí)間延遲單元或移相器的分辨率是有限的。這通常利用離散時(shí)間（或相位）步長(zhǎng)來(lái)實(shí)現(xiàn)數(shù)字控制。但是，如何確定延遲單元或移向器的分辨率或位數(shù)，以達(dá)到的所需的波束質(zhì)量呢？

 

與常見(jiàn)的理解相反，波束角度分辨率并不等于移相器的分辨率。從方程式1（第二部分中的方程式2）中，我們可以看出這樣的關(guān)系：

 

 

我們可以用整個(gè)陣列中的相移來(lái)表達(dá)這種關(guān)系，需要將陣列寬度D替換為元件間隔d。然后如果我們將移相器ΦLSB 替換為?Φ,我們可以粗略估算波束角度分辨率。對(duì)于N個(gè)元件以半個(gè)波長(zhǎng)間隔排列的線性陣列來(lái)說(shuō)，波束角度分辨率如方程式2所示。

 

 

這是背離瞄準(zhǔn)線的波束角度分辨率，描述了當(dāng)陣列的一半相移為零，另一半的相移為移相器的LSB時(shí)的波束角度。如果不到一半的陣列通過(guò)編程達(dá)到相位LSB，則角度可能更小。圖4顯示使用2位移相器的30元件陣列的波束角度（相位LSB逐漸增加）。注意，波束角度增加，直到一半元件移相LSB，然后在所有元件移相LSB時(shí)歸零。當(dāng)波束角度通過(guò)陣列中的相位差而變化時(shí)，這是有意義的。注意，正如前面計(jì)算的那樣，此特性的峰值為θRES。

 

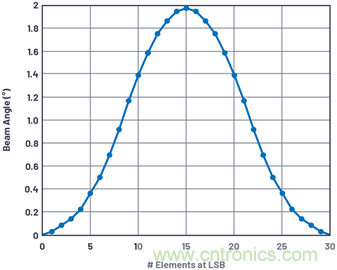
圖4.30元件線性陣列在LSB時(shí)的波束角度與元件數(shù)量之間的關(guān)系。

 

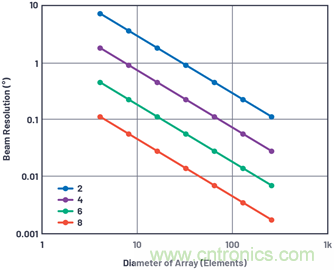
圖5.移相器分辨率為2位至8位時(shí)，波束角度分辨率與陣列大小的關(guān)系。

 

圖5顯示不同移相器分辨率下θRES與陣列直徑（元件間隔為λ/2）的關(guān)系。這表明，即使是LSB為90°的非常粗糙的2位移相器，也可以在直徑為30個(gè)元件的陣列中實(shí)現(xiàn)1°的分辨率。在第一部分使用方程式10針對(duì)30元件、λ/2間隔條件進(jìn)行求解時(shí)，主瓣波束寬度約為3.3°，表示即便使用這個(gè)非常粗糙的移相器，我們也具備足夠的分辨率。那么，使用更高分辨率的移相器又會(huì)得出什么結(jié)果？從時(shí)間采樣系統(tǒng)（數(shù)據(jù)轉(zhuǎn)換器）和空間采樣系統(tǒng)（相控陣天線）之間的類比可以看出，較高分辨率的數(shù)據(jù)轉(zhuǎn)換器產(chǎn)生較低的量化本底噪聲。更高分辨率的相位/時(shí)間偏移器會(huì)導(dǎo)致較低的量化旁瓣電平(QSLL)。

 

圖6顯示之前描述的編程采用θRES波束分辨率角度的2位30元件線性陣列的移相器設(shè)置和相位誤差。一半陣列設(shè)為零相移，另一半設(shè)為90°LSB。注意，誤差（理想量化相移與實(shí)際量化相移之間的差異）曲線呈鋸齒狀。

 

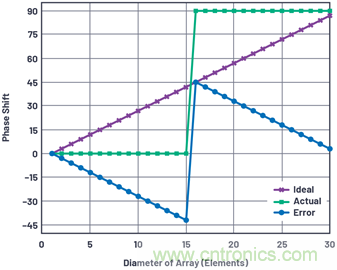
圖6.陣列中的元件相移和相位誤差。

 

圖7顯示同一天線在轉(zhuǎn)向0°和轉(zhuǎn)向波束分辨率角度時(shí)的天線方向圖。請(qǐng)注意，由于移相器的量化誤差，出現(xiàn)了嚴(yán)重的方向圖退化。

 

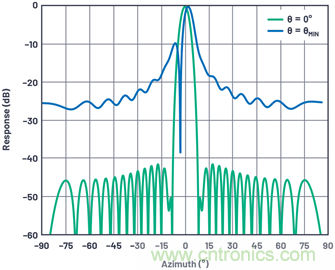
圖7.在最小波束角度下具有量化旁瓣的天線方向圖。

 

當(dāng)孔徑內(nèi)發(fā)生最大量化誤差，其他所有元件都是零誤差，且相鄰元件間隔LSB/2時(shí)，出現(xiàn)最糟糕的量化旁瓣情形。這代表了最大可能的量化誤差和孔徑誤差的最大周期。圖8顯示了使用2位30元件時(shí)的這種情況。

 

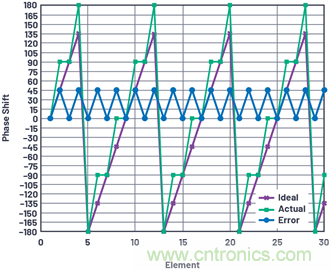
圖8.最糟糕的天線量化旁瓣情形——2位。

 

這種情況在可預(yù)測(cè)的波束角度下（如方程3所示）發(fā)生。

 

 

其中 n < 2BITS,且n為奇數(shù)。對(duì)于2位系統(tǒng)，這種情況會(huì)在±14.5°和±48.6°范圍之間發(fā)生4次。圖9顯示該系統(tǒng)在n = 1，q = +14.5°時(shí)的天線方向圖。注意在–50°時(shí)具有明顯的–7.5 dB量化旁瓣。

 

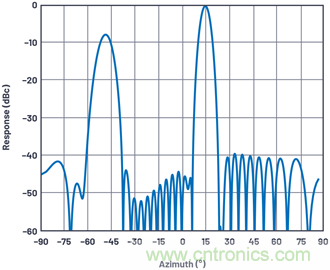
圖9.最糟糕的天線量化旁瓣情形：2位，n = 1，30元件。

 

除了量化誤差依次為0和LSB/2的特殊情況外，在其他波束角度下，rms誤差隨著波束在孔徑上的擴(kuò)散而減小。事實(shí)上，對(duì)于n為偶數(shù)值的角度方程（方程式3），量化誤差為0。如果我們繪制在不同移相器分辨率下最高量化旁瓣的相對(duì)電平，會(huì)出現(xiàn)一些有趣的方向圖。圖9顯示100元件線性陣列最糟糕的QSLL，該陣列使用海明錐形，以便將量化旁瓣與本節(jié)前面討論的經(jīng)典開(kāi)窗旁瓣區(qū)分開(kāi)來(lái)。

 

注意，在30°時(shí)，所有量化誤差都趨于0，這可以顯示為sin(30°) = 0.5時(shí)的結(jié)果。請(qǐng)注意，對(duì)于任何特定的n位移相器，在最糟糕電平下的波束角度在更高分辨率n下會(huì)顯示零量化誤差。在這里可以看出描述的最糟糕旁瓣電平下的波束角度，以及QSLL在每位分辨率下改善了6 dB。

 

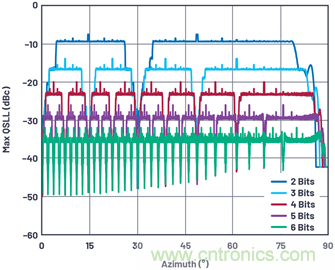
圖10.在2位至6位移相器分辨率下，最糟糕的量化旁瓣與波束角度的關(guān)系。

 

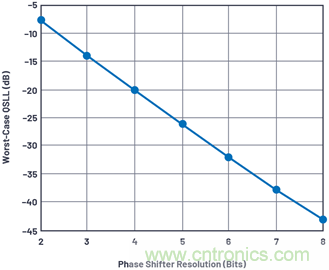
圖11.最糟糕的量化旁瓣電平與移相器分辨率的關(guān)系。

 

2位至8位移相器分辨率的最大量化旁瓣電平QSLL如圖11所示，它遵循類似的數(shù)據(jù)轉(zhuǎn)換器量化噪聲規(guī)律，

 

 

或每位分辨率約6 dB。在2位時(shí)，QSLL電平約為-7.5 dB，高于數(shù)據(jù)轉(zhuǎn)換器進(jìn)行隨機(jī)信號(hào)采樣時(shí)經(jīng)典的+12 dB。這種差異可以視為在孔徑采樣時(shí)周期性出現(xiàn)的鋸齒誤差導(dǎo)致的結(jié)果，其中空間諧波會(huì)增加相位。注意QSLL與孔徑大小不呈函數(shù)關(guān)系。

 

總結(jié)

 

我們現(xiàn)在可以總結(jié)出天線工程師面臨的與波束寬度和旁瓣相關(guān)的一些挑戰(zhàn)：

 

●   角度分辨率需要窄波束。窄波束需要大孔徑，這又需要許多元件。此外，波束在背離瞄準(zhǔn)線時(shí)會(huì)變寬，所以需要額外的元件，以在掃描角度增大時(shí)保持波束寬度不變。

 

●   似乎可以通過(guò)增大元件間隔來(lái)擴(kuò)大整個(gè)天線區(qū)域，而無(wú)需額外增加元件。此舉可以讓波束變窄，但是，很遺憾，如果元件分布不均，會(huì)導(dǎo)致產(chǎn)生柵瓣?？蓢L試通過(guò)減小掃描角度，同時(shí)采用有意隨機(jī)顯示元件方向圖的非周期陣列，來(lái)利用增加的天線區(qū)域，同時(shí)最大限度減少柵瓣問(wèn)題。

 

●   旁瓣是另一個(gè)問(wèn)題，我們已知可以通過(guò)將陣列增益朝向邊緣逐漸減小來(lái)解決。但是，這種錐削以波束變寬為代價(jià)，又會(huì)需要更多元件。移相器分辨率會(huì)導(dǎo)致出現(xiàn)量化旁瓣，在設(shè)計(jì)天線時(shí)也必須加以考慮。對(duì)于采用移相器的天線，波束斜視現(xiàn)象會(huì)導(dǎo)致角位移與頻率相互影響，從而限制高角度分辨率下可用的帶寬。

 

以上就是有關(guān)相控陣天線方向圖全部三個(gè)部分的內(nèi)容。在第一部分中，我們介紹波束指向、陣列因子和天線增益。在第二部分中，我們討論柵瓣和波束斜視的缺點(diǎn)。在第三部分中，我們討論錐削和量化誤差。本文不是針對(duì)精通電磁和輻射元件設(shè)計(jì)的天線設(shè)計(jì)工程師，而是針對(duì)在相控陣領(lǐng)域工作的大量相鄰學(xué)科的工程師，這些直觀的解釋，將有助于他們理解影響整個(gè)天線方向圖的性能的各種因素。

 

參考電路

 

Balanis, Constantine A. 天線理論、分析和設(shè)計(jì)。第3版，Wiley，2005年。

 

Mailloux, Robert J. 相控陣天線手冊(cè)。第2版。Artech House，2005年。

 

O’Donnell, Robert M. “雷達(dá)系統(tǒng)工程：簡(jiǎn)介。” IEEE，2012年6月。

 

Skolnik, Merrill. 雷達(dá)手冊(cè)。第3版，McGraw Hill，2008年。

 

 

推薦閱讀：