【導(dǎo)讀】對于線性電源來說，穩(wěn)定性是較為重要的。本篇文章針對一些線性電源資料當(dāng)中出現(xiàn)的矛盾點進(jìn)行分析和解釋，是一篇較好的思路指導(dǎo)類文章，希望能在大家設(shè)計的道路上有所幫助。
線性電源能夠?qū)⒔涣麟娹D(zhuǎn)換為直流電，而想要得到較為精準(zhǔn)的直流電壓，則需要經(jīng)過穩(wěn)壓電路進(jìn)行穩(wěn)壓。也就是說，對于線性電源來說，穩(wěn)定性是較為重要的。本文將針對線性電源的環(huán)路穩(wěn)定性進(jìn)行了探討。
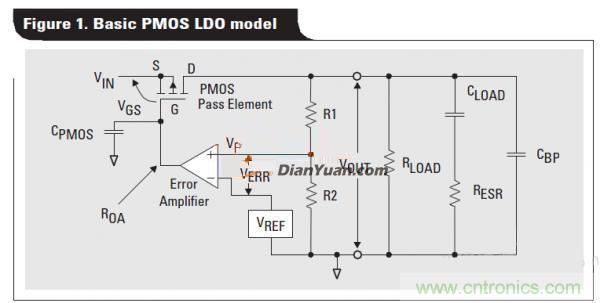
圖1：線性電源的等效模型模型
線性電源的等效模型模型如圖1所示， 穩(wěn)定直接如圖可知，電路的三個極點和一個零點，即得到開環(huán)傳遞函數(shù)Gop，GEA是誤差放大器的增益，GFB是反饋環(huán)路的增益，GPMOG是PMOS的增益。
那么下面這幾個公式當(dāng)中的參數(shù)是如何做到的呢?根據(jù)PMOS的小信號模型，g是PMOS的跨導(dǎo)，Ro是輸出等效電阻，傳遞函數(shù)不應(yīng)該是Uo/Ugs=gRo?
The resulting expressin for open-loop gain is
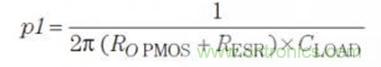
The second pole(p2) is due to the output capacitance ESR (R ESR) and the estimated bypass capacitance,CBP.
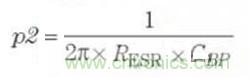
The third pole(p3) is due to the erro anplifier output resistance(ROA) and the equivalent PMOS capacitance (CPMOS).
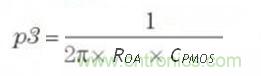
The single zero (Z1) is derived from the output capacitance ESR(RESR)and the output capacitance(CLOAD).
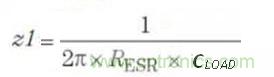
上面說的這些公式，雖然是從國外的參考資料上弄來的，但PMOS依然可以工作在飽和和線性兩種方式，兩者的零極點是不同的。這些應(yīng)該是飽和方式的零極點，與LDO的本意出現(xiàn)矛盾。
LDO的PMOS應(yīng)該工作在線性方式，此時的零極低公式，比飽和方式的復(fù)雜的多，而且與Rl有關(guān)。所以這個，也是概念不清的。雖然PMOS飽和方式的零極點公式很可能是對的。概念不清之二就是，沒有開環(huán)放大倍數(shù)。總之，沒有一個清晰的概念，和認(rèn)真負(fù)責(zé)的計算方法，就不可能得到正確的傳遞函數(shù)。
總的來說，這個資料上的公式雖然并不完全不正確，但是很有可能屬于歪打正著的類型。線性方式比飽和方式要復(fù)雜。而且借用了飽和方式的gm概念。線性方式的gm，并無此概念，但為方便計算，沿用飽和方式的叫法。
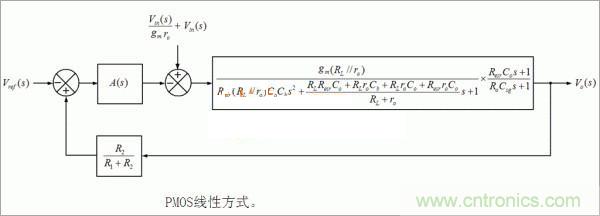
圖2：PMOS線性方式
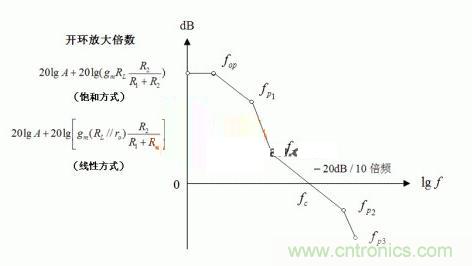
想分析頻率特性，必須給出開環(huán)傳遞函數(shù)，誰能做到這一點，誰就是正確的，誰做不到，誰就得不到正確答案。
在飽和方式，gm也不是一成不變的，但看作不變的。就像三極管公社放大電路，把beta看作恒定一樣。在線性方式，Rds也不是一成不變的，但看作不變的，根據(jù)一個具體或特殊設(shè)計的PMOS，可以保證，在額定電流或最大最小負(fù)載的情況下，Rds變化很小。
有一個臨界電壓，Vds，來區(qū)分線性和飽和狀態(tài)。例如定義Vds為1V左右，小于1V為線性電阻，而高于1V為飽和方式。
在線性電阻方式，依然沿用飽和關(guān)系式，也有g(shù)m，這個gm可以通過線性關(guān)系式求導(dǎo)得到。但這依然要求Vds恒定，也就是說，計算線性方式的傳函，要固定Vds。例如1V。
按照這樣的方法，可以把變化的Vds，看作Vin的擾動，穩(wěn)定性依然可以得到保證。作為LDO的設(shè)計，必須同時都要滿足線性和飽和方式的穩(wěn)定性能，還要保證最大最到負(fù)載的穩(wěn)定性能。Vin的變化，作為負(fù)載擾動，只要頻率的補償保證了上述條件下的問題，那么負(fù)載擾動也一定是穩(wěn)定的。
按照電路模型，計算的開環(huán)傳遞函數(shù)是沒有問題的。但計算零極點要用近似計算法，開路時間常數(shù)法，你看看相關(guān)資料就知道了。超過3階就沒有解析解了，怎么算呢?這是計算機仿真應(yīng)該做的。
本篇文章針對一些線性電源資料當(dāng)中出現(xiàn)的矛盾點進(jìn)行分析和解釋，是一篇較好的思路指導(dǎo)類文章。大家在遇到不明白的問題或者疑問時，向別人請教或者思考一下是一種非常好的習(xí)慣，能幫助大家在設(shè)計的道路上飛速成長。
